Ubuntu-fr

wiscot

Re : Topic des couche tard (26).

@ tshirtman: et le pc ? Bon ou pas ?

tshirtman

Re : Topic des couche tard (26).

@wiscot: la transplantation d'écran? oui c'est cool j'ai un peu galéré a remettre la facade (je vois pas comment on est sensé faire sans forcer, peut être en démontant tout le reste de la coque...)

là j'ai mis mes deux eeepc sur le bureau avec un écran externe sur chaque, et synergy entre les deux, du coup j'ai 19" + 15" c'est assez confortable .

et je suis content d'avoir un eeepc 100% opérationel aussi ^^ j'ai même retrouvé comment j'avais configuré wmii pour changer la résolution sans soucis... faut éditer /usr/share/sessions/wmii.desktop et mettre wmiiwrapper au lieu de wmii, wmiiwrapper étant un script préalablement créé contenant

#!/bin/sh
while true
do wmii
done

du coup quand je regle ma résolution avec xrandr je peut faire alt-a quit ou kill wmii et il se relance en bonne taille

Dernière modification par tshirtman (Le 18/07/2009, à 20:31)

---

Le blog de tshirtman, du python, du shell, du libre, et d'autres choses.
Mon petit frère écrit des trucs biens!
Ultimate smash friends, un smash bros like, libre paquet natty!

philarmonie

Re : Topic des couche tard (26).

"ce groupe n'est pas un groupe car ses membres n'ont pas d'inverses"

Bon y'a qu'un matheux pour rire à ce type de blague. ^^

Pour faire simple : un groupe c'est des objets que tu peux ajouter et soustraire entre eux.

Pour faire compliqué : un groupe est la donné d'un ensemble G et d'une loi interne que je vais noter +, et mon groupe sera noté (G, +). Cette loi interne est en fait une fonction de GxG dans G qui doit vérifier certaines propriétés pour que la structure (G, +) soit un groupe :
- il y a un élément neutre, noté ici 0, tel que pour tout x dans G on est : x + 0 = x
- + est associative, i.e pour touut x,y et z dans G on a : x +( y + z ) = (x + y ) + z
- tout élément à un inverse, i.e pour tout x dans G il existe y dans G tel que x + y = 0

Si on n'a pas l'existence d'un inverse on obtient ce qu'on appelle un monoïde ce le cas de (ℕ, +) (l'ensemble des entiers naturels avec son addition usuelle). Pour faire de cette structure un groupe on a rajouté un inverse pour chaque entier est on a obtenu (ℤ, +) (les entiers relatifs avec leur addition usuelle).

Maintenant la notion d'isomorphisme. Tu prends deux groupes (G, +) et (G', +'). Un isomorphisme est une bijection f de G dans G' qui respecte leur loi interne, i.e :
- f(0) = 0' (l'élément neutre de G est associé à l'élément neutre de G')
- f(x+y) = f(x) +' f(y)  (faire "l'addition" au départ ou à l'arrivée ne change rien, ça respecte les lois internes).
Edit : seule la deuxième condition suffit en fait, la première en étant une conséquence.

En fait deux groupes isomorphes sont une seule est même entité mathématique. Ça signifie que les deux structures sont identiques même si les "objets" sur lesquelles elles sont construites sont différentes.
Quand on conçoit les objets mathématiques en terme de structure (un groupe est une structure, ici algébrique, parmi d'autres) l'isomorphisme signifie l'égalité. C'est pour cela que j'ai fait référence à la notion d'isomorphisme quand je parlais du rapport entre la géométrie plane et les complexes.

L'isomorphisme le plus connu est la fonction logarithme qui transforme la multiplication en addition.
(ℝ⁺*, x) (les réels positifs non nuls munis de la multiplication) est un groupe, et (ℝ, +) (les réels munis de l'addition) est un autre groupe. Et ces deux groupes sont identiques, la fonction logarithme réalisant un isomorphisme entre eux.

J'espère ne pas avoir était trop abstrait dans mon discours. ^^

Dernière modification par philarmonie (Le 18/07/2009, à 20:40)

wiscot

Re : Topic des couche tard (26).

@wiscot: la transplantation d'écran? oui c'est cool j'ai un peu galéré a remettre la facade (je vois pas comment on est sensé faire sans forcer, peut être en démontant tout le reste de la coque...)

là j'ai mis mes deux eeepc sur le bureau avec un écran externe sur chaque, et synergy entre les deux, du coup j'ai 19" + 15" c'est assez confortable .

Nice

tshirtman

Re : Topic des couche tard (26).

(faire "l'addition" au départ ou à l'arrivée ne change rien, ça respecte les lois internes).

j'allais te dire que tu t'étais planté ^^, belle anticipation ^^

sinon merci, c'est limpide

edit: ah tu  as déplacé la ' ce qui signifie que j'avais mal compris ^^, mais je crois que c'est bon

Dernière modification par tshirtman (Le 18/07/2009, à 20:39)

---

Le blog de tshirtman, du python, du shell, du libre, et d'autres choses.
Mon petit frère écrit des trucs biens!
Ultimate smash friends, un smash bros like, libre paquet natty!

compte supprimé

Re : Topic des couche tard (26).

J'ai vu, pour Grunt... triste...
Un volontaire pour nous coder une appli flash qui fasse une minute de silence ?

"Ceuuuh n'est qu'un auuurevoooir..."
Pour l'appli flash, le jour ou Stallman utilisera vim

philarmonie

Re : Topic des couche tard (26).

sinon merci, c'est limpide

Merci, j'avais peur d'avoir fait trop théorique.
Mais bon, comme tu codes et la notion de structure étant finalement assez similaire à celle d'objets (au sens de la programmation), je me suis dit que je pouvais me le permettre.

Dernière modification par philarmonie (Le 18/07/2009, à 20:53)

tshirtman

Re : Topic des couche tard (26).

J'ai une limite en abstraction aussi, mais c'est un peu en espérant la repousser que je reprends les maths ^^.

mais oui avec la prog objet, c'est tout à fait clair la façon dont tu as expliqué

Dernière modification par tshirtman (Le 18/07/2009, à 20:55)

---

Le blog de tshirtman, du python, du shell, du libre, et d'autres choses.
Mon petit frère écrit des trucs biens!
Ultimate smash friends, un smash bros like, libre paquet natty!

Compte supprimé

Re : Topic des couche tard (26).

C'est pas avec ce genre de post que je risque de devenir mathématicien moi...

le pire c'est que je reprends les maths en L3 (infos pas maths pas fou non plus) en septembre et que là ils m'ont limite démotivé xD

sinon le nombre i tel que i² = -1 (qu'on ne peut pas appeler la racine carrée de -1 (hein spatz! )) est le nombre "de base" des irréels, tous ses multiples sont des irréels, en gros 3i est un nombre irréel (ou imaginaire) et 5i+2 est un nombre "complexe" (une partie réelle et une partie imaginaire).

i n'est pas la racine carrée de -1 attention :
il y a deux racines carrées pour -1 ... -i et i
i est l'une des racines carrées de -1

kouskous

Re : Topic des couche tard (26).

---

#!/usr/bin/killall
« « J'aime kouskous » — kouskous. »  — kouskous.

Compte supprimé

Re : Topic des couche tard (26).

(putain, je pose une petite question complètement innocente et futile, trois jours après ils sont encore en train de troller dessus )

Pourquoi futile ?
philarmonie dit qu'il y a autant d'entiers positifs que d'entiers relatif c'est à dire l'infini pour lui.
Vois-tu tout l'univers lorsque tu ne regardes qu'en direction de la pleine lune dans le ciel la nuit ?
Ou juste une portion de l'univers ?

Dernière modification par Compte supprimé (Le 18/07/2009, à 21:20)

philarmonie

Re : Topic des couche tard (26).

mais oui avec la prog objet, c'est tout à fait clair la façon dont tu as expliqué

Tiens j'ai réfléchi depuis et j'aurai pu l'expliquer comme ça aussi.
Il me semble qu'en C++ la bibliothèque Qt réimplémente le type string de la bibliothèque standard. Et bah caster un Qstring en string, ou vice versa, c'est appliquer un isomorphisme.

didrocks

Re : Topic des couche tard (26).

Et kinouchou tu as le temps de poster pendant la journée alors que tu es entourée de monde ??? C'est un pure scandale

Plus sérieusement, j'espère que ce n'est pas trop dur là-bas et que vous pouvez vous reposer

spatz

Re : Topic des couche tard (26).

Bonsoir. . A ce que je vois l'admin est devenu accro au TdCT .

---

PLOP ! Blogueur ! Râleur ! Agnostique ! Architecte ! Floodeur ! Gentil ! Chiant ! Fourbe ! Crâneur ! GNU/Windows/Linuxien ! Machiavélique ! Beau ! Républicain ! Intelligent ! Bosseur ! Très Prétentieux ! Scientifique ! Frimeur ! Étudiant !  De bonne foi ! Perverti ! Ubunteros ! Grand ! Sociable! Altruiste ! Provoc' ! Censé !

Toineo

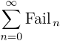
Re : Topic des couche tard (26).

@philarmonie : je confirme, ton explication est très claire

J'sort d'un diner interminable... Trop lourd...

---

Fail

tshirtman

Re : Topic des couche tard (26).

C'est pas avec ce genre de post que je risque de devenir mathématicien moi...

le pire c'est que je reprends les maths en L3 (infos pas maths pas fou non plus) en septembre et que là ils m'ont limite démotivé xD

sinon le nombre i tel que i² = -1 (qu'on ne peut pas appeler la racine carrée de -1 (hein spatz! )) est le nombre "de base" des irréels, tous ses multiples sont des irréels, en gros 3i est un nombre irréel (ou imaginaire) et 5i+2 est un nombre "complexe" (une partie réelle et une partie imaginaire).

i n'est pas la racine carrée de -1 attention :
il y a deux racines carrées pour -1 ... -i et i
i est l'une des racines carrées de -1

hey c'est pas à moi qu'il faut dire ça! j'ai dit "soit i tel que i² = -1" j'ai pas de définition plus rigoureuse! ensuite tu oublie la définition de racine carrée: des deux valeurs possibles c'est la valeur positive qui est la "racine carré". (bon reste à savoir si c'est i ou -i qui est positif! philarmonie un avis la dessus?

philarmonie dit qu'il y a autant d'entiers positifs que d'entiers relatif c'est à dire l'infini pour lui.
Vois-tu tout l'univers lorsque tu ne regarde qu'en direction de la pleine lune dans le ciel la nuit ?
Ou juste une portion de l'univers ?

un sous ensemble infinie d'un ensemble infinie, ne confond pas infinie et univers, on peut faire une  bijection de deux ensembles infinie l'un dans l'autres sans qu'ils soient de même cardinalité (si j'ai bien tout compris).

@spatz: justement je le trouvais un peu absent moi!

---

Le blog de tshirtman, du python, du shell, du libre, et d'autres choses.
Mon petit frère écrit des trucs biens!
Ultimate smash friends, un smash bros like, libre paquet natty!

compte abandonné

Re : Topic des couche tard (26).

Les maths c'est indigeste...

Dernière modification par Pоlydеsmе (Le 18/07/2009, à 21:31)

wiscot

Re : Topic des couche tard (26).

Les maths c'est indigeste...

+1 pourtant j'étais .....

wiscot

Re : Topic des couche tard (26).

@pierguiard: Tu m'as toujours pas répondu /pourquoi pas Lenevo????

Dernière modification par wiscot (Le 18/07/2009, à 21:45)

samυncle

Re : Topic des couche tard (26).

---

Hello world

Dr Le Rouge

Re : Topic des couche tard (26).

tshirtman a écrit :
on peut faire une  bijection de deux ensembles infinie l'un dans l'autres sans qu'ils soient de même cardinalité (si j'ai bien tout compris).

Euh... non.
En fait, on dit de deux ensembles qu'ils ont même cardinaux si et seulement si il y a une bijection de l'un dans l'autre.
Donc card(N)=card(Z)
"C'est deux infinies de même taille" en quelque sorte, et ce quand bien même c'est totalement contre-intuitif.

Cet instant matheux vous a été offert par LeRouge inc.

Dernière modification par Dr Le Rouge (Le 18/07/2009, à 21:53)

---

C'est deux suites de Cauchy qui veulent aller à la soirée 'no limit'. Hélas, à l'entrée le videur leur dit : "désolé, c'est complet !".
mon site perso (π²/6.fr) et mon blog

kinouchou

Re : Topic des couche tard (26).

pour le stand la journée aux vieilles charrues se termine, le plus dur ça va être d'empêcher les gens de rentrer.
La journée a été un succès.

En plus sur le stand on a des démonstration de Musique assistée sur ordi et l'ambiance est très sympa.

bonne nuit à tous et bon week-end

tshirtman

Re : Topic des couche tard (26).

tshirtman a écrit :
on peut faire une  bijection de deux ensembles infinie l'un dans l'autres sans qu'ils soient de même cardinalité (si j'ai bien tout compris).

Euh... non.
En fait, on dit de deux ensembles qu'ils ont même cardinaux si et seulement si il y a une bijection de l'un dans l'autre.
Donc card(N)=card(Z)
"C'est deux infinies de même taille" en quelque sorte, et ce quand bien même c'est totalement contre-intuitif.

Cet instant matheux vous a été offert par LeRouge inc.

ah mince xD j'avais crus comprendre qu'on pouvait faire une bijection dans deux infinis de taille différentes, mais en fait je vois mon erreur c'est justement le contraire qui a été dit plus tôt... >_>

---

Le blog de tshirtman, du python, du shell, du libre, et d'autres choses.
Mon petit frère écrit des trucs biens!
Ultimate smash friends, un smash bros like, libre paquet natty!

compte supprimé

Re : Topic des couche tard (26).

Les maths ça roxx !
(Même si pour l'instant j'en suis qu'aux fonctions... Y'aurais pas un équivalent de la "Wikiversité" pour prendre de l'avance ?)

EDIT : Bonne nuit !

Dernière modification par Lagierl (Le 18/07/2009, à 22:11)

philarmonie

Re : Topic des couche tard (26).

philarmonie un avis la dessus?

Oui, i est une racine carré de-1... ainsi que -i.
Habituellement on ne définit pas de fonction √ sur ℂ, mais on définit bien la notion de racine carré ainsi:
une racine carré d'un complexe Z est un complexe z tel que z² = Z.
et tout complexe a deux racines carrés opposés (edit : sauf zéro)

philarmonie dit qu'il y a autant d'entiers positifs que d'entiers relatif c'est à dire l'infini pour lui.

Je n'ai pas dit que c'était l'infini mais UN infini, et c'est le plus petit de tous : l'infini dénombrable (noté généralement Alpeh0 (je ne sais pas faire la lettre Aleph)).

un sous ensemble infinie d'un ensemble infinie, ne confond pas infinie et univers, on peut faire une  bijection de deux ensembles infinie l'un dans l'autres sans qu'ils soient de même cardinalité (si j'ai bien tout compris).

Non. Justement, c'est l'existence d'une bijection entre deux ensembles qui en fait des ensembles de même cardinalité. S'ils n'ont pas même cardinalité on ne peut pas faire de bijection entre les deux. Exemple : ℕ et ℝ sont tous les deux infinis mais n'ont pas même cardinalité.
Il y a aussi des règles de calculs "spéciales" en arithmétique transfinie :
si A et B sont deux cardinaux infinis alors A + B = A * B = max(A, B)
si A est infini et n est fini alors n^A est indéterminable, mais plus grande que A.

La première règle implique que card(ℝ) = card(ℝ²), i.e qu'il y a autant de points sur une droite que dans un plan (le fameux résultat de Cantor « qu'il voyait mais ne croyait pas »).
D'ailleurs avec ces règles, on peut montrer que card(ℕ) = card(ℤ) = card(ℚ) et card(ℕ) < card(ℝ)

Dernière modification par philarmonie (Le 18/07/2009, à 22:07)